 |
|
|
Tradução, organização e notas de Frederico Denez e Gustavo Capobianco Volaco
Aula 2
12 de Dezembro de 1978
Eu me aventurei a anunciar que talvez tomaria um exemplo do que se chama o borromeu generalizado, a saber que eu enunciaria de que maneira se pode virar borromeu, quero dizer, a partir de qual momento se prova borromeu um número de cinco círculos, dado que no borromeu é de círculos que se trata. O borromeu generalizado, o havia anunciado para dois círculos retirados em cinco. A solução me foi entregue em mãos por duas pessoas, a saber, Madame Parizot que espero esteja aqui presente, e um chamado Vappereau, que também queria contribuir para essa solução.
Não há nada mais fácil do que virar borromeu, quer dizer, desencadear, quer dizer, liberar cinco círculos. E aqui um, e aqui dois, e aqui o terceiro, aqui o quarto e aqui o quinto. Esse é o terceiro, esse é o segundo. O segundo é violeta, o terceiro é bege, o quarto é verde e o quinto é vermelho. A maneira de liberar dois círculos em cinco é bastante clara. As pessoas que se enredaram com isso gentilmente, uma e outra, disseram de que maneira é possível: é possível de dez maneiras. É suficiente liberar, quer dizer, cortar o 1 e o 2, o 1 e o 3, o 1 e o 4, o 1 e o 5 os outros três se desencadeiam, como é fácil de ver pelo fato de que o violeta ali, por exemplo, enlaça até se reduzir a alguma coisa que vem lá. Esse violeta se reduz a alguma coisa que desliza até lá e que, pelo fato de ter desaparecido o 5, resta desanodado do verde, do bege e do violeta. Isto resta livre, estes três, dado que se trata aqui de círculos, estes três círculos estão livres um em relação ao outro. O verde, o violeta e o bege estão livres em relação ao violeta, a saber, que o verde se desanoda, o bege se desanoda também e o violeta aqui se desanoda igualmente. É fácil ver que desanodado o 2 associado ao 3, o 2 associado ao 4, o 2 associado ao 5, teremos o mesmo resultado. O 3 associado ao 4 e o 3 associado ao 5 teremos o mesmo resultado, o 4 associado ao 5 terá também o mesmo resultado. Existe, portanto, dez maneira de seccionar um desses círculos que são cinco, de seccioná-los de uma maneira tal que o resultado seja alcançado.
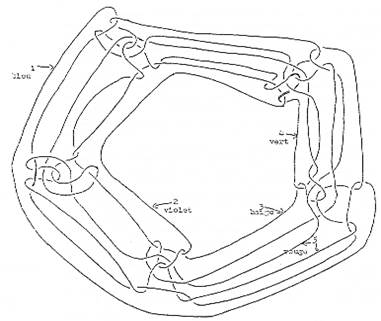
Me deixei levar para mais longe em minha investigação, a saber, me questionei sobre um grupo de seis círculos, e questionei sobre a maneira de como se obtêm um borromeu generalizado ao se cortar três deles. Há efetivamente 35 maneira de fazer isso. Para isso, teríamos que, da mesma maneira que fazemos esses cinco círculos, produzir um sexto. Desta maneira os dispenso, já que seria um pouco forçado. Mas é possível construí-lo. Entre as 35 maneiras de cortar os três círculos obtendo esse nó que chamo borromeu, dado que está simbolizado a partir de três, quer dizer que os três restam desanodados quando se retira um... é suficiente cortar um para que os outros três restem desanodados.
No borromeu de seis, basta igualmente cortar um para que os seis restem desanodados. Eu especifico que existem dez maneiras de desanodar cinco círculos e que há trinta e cinco maneiras de desanodar seis círculos cortando três deles. Talvez eu distribua o que se conseguiu obter esta manhã por Soury que concordou em se encarregar de fotocopiá-lo de uma foto colorida, quer dizer, que as cores não aparecem, mas que, ao cortar três desses círculos, se pode perceber que os outros três restam livres. Isso demanda um certo cuidado para colorir cada um desses círculos. Mas se pode ver que isso funciona. Isto supõe que se retirem a princípio 2 e, em seguida, um terceiro. É no terceiro que cada um desses círculos passa a ser livre.
É você Vappereau? Eu te escuto.
Vappereau: – Você cometeu um erro na maneira de contar as diferentes maneiras de desanodar a cadeia de seis cortando três. Você apresentou o resultado para a cadeia de sete cortando quatro, quer dizer 35...
Lacan: – Eu disse que cortando três sobre os seis se obtêm uma cadeia borromeana...
Vappereau: – Você disse que há 35 maneiras de fazê-lo, mas não há mais que 20...
Lacan: – Sim, é verdade que não há mais que 20. É verdade que há mais que 20 e que, devido a isso, me equivoquei. E bem, me resta pedir desculpas e lhe prometer que, da próxima vez, não lhe entreterei com esse círculos. Bem, adeus! (1)
Notas
(1) Esses dois desenhos e a série de números estão, nas versões que utilizamos para produzir esta, na parte final desta aula. Preferimos, contudo, coloca-la já no início pois, ao que tudo indica, eles jã estavam no quadro quando Lacan começou a falar.