Acheronta 30 - A topología e o tempo - Tradução, organização e notas de Frederico Denez e Gustavo Capobianco Volaco

Tradução, organização e notas de Frederico Denez e Gustavo Capobianco Volaco

Nasio (1): – Parece que subir neste tablado conduz quase automaticamente a lhes solicitar, a vocês, os ouvintes do Seminário de Lacan, indulgência. Pois foi somente ontem, segunda-feira, ao meio-dia, que Lacan me solicitou para que lhes falasse de uma questão que lhe havia feito. Ela concerne à teoria do sujeito do inconsciente. Se eu fosse intitular esta intervenção escreveria: "A criança Magnífica da Psicanálise".

Quando, no início do ano, meu projeto era estudar a articulação entre o saber inconsciente e a interpretação, progressivamente, conforme certos desenvolvimentos, a questão do sujeito tomou a dianteira e se tornou o problema principal. Esta manhã, vou me limitar a uma evocação sucinta das abordagens possíveis do conceito de sujeito - abordagens certamente conhecidas pela maioria de vocês - a fim de submeter, em seguida, alguma interrogações.

Dividamos este resumo em três partes, de acordo com a relação do sujeito ao saber inconsciente, de acordo com a relação do sujeito à lógica de Frege (2) e, enfim, de acordo com a relação do sujeito e a castração.

I - Nosso ponto de partida será o da psicanálise mesmo, constituído por esse fato de linguagem que se enuncia assim: "eu não sei o que eu digo". Se o desejo da histérica é fundados da transferência, o "eu não sei o que eu digo" é o fato fundador da noção de inconsciente em Freud e da noção de inconsciente como saber em Lacan.

Assim, "eu não sei o que eu digo". Eu não sei o quê? Eu não sei o que eu digo é um significante e que, como tal, não se dirige ao ser falante, mas a um outro significante. Se dirige ao Outro. Falo, emito sons, construo sentidos mas, o dito, ele, me escapa. Me escapa porque não está em poder do sujeito o saber com que outro dito, esse dito irá se ligar. "O significante se endereça ao Outro" quer dizer que ele vai se ligar com outro significante, alhures, ao lado, em seguida. Assim, Eu não sei o quê? O efeito de minha palavra sobre você. Sobre o Outro. E por não saber o que eu digo, eu digo mais do que sou.
Em uma palavra, eu não sei o que eu digo, porque o meu dito segue alhures, sem eu saber se endereça ao Outro e, sem que eu saiba também, me vem do Outro. Ele vem do Outro e se endereça, ele parte do Outro.
Existe ainda uma razão para esse "eu não sei o que eu digo". É que o sujeito que enuncia seu dito - insisto, o sujeito que enuncia - não é o mesmo quando a mensagem, o dito, pode retornar. Não somos mais o mesmo, porque no ato de dizer, mudamos. A expressão "sujeito efeito do significante" quer dizer justamente que o sujeito muda com o ato de dizer.

Em resumo, eu não sei o quê? (frase ilegível (3) )
1 - Eu não sei que estava ali, sob tal significante. Que tal dito era o significante, meu significante, o significante do sujeito. Então, lá estava ele, um ponto de não saber. E esse ponto de não saber representa o que escapa ao Outro e que se endereça a ele.
2 - Por não saber qual é o significante sob o par que eu me encontrava, ignoro simultaneamente o outro significante ao qual ele se endereça. Dito de uma outra maneira: eu não sei, dizendo, qual significante me espera.
3 - Não sei quem eu sou.

Em suma, vocês tem por um lado o sujeito fixado, suspenso à um significante, aquele de seu ato de dizer. Por outro lado os significantes se sucedem um atrás do outro, o sujeito, de fato, não está em nenhuma parte. Repito, pois é a conclusão a que eu queria chegar: o sujeito está em no ato, seu ato de enunciar o dito mas, sendo que este vem do Outro e se dirige ao Outro, que tudo ocorre entre ditos, o sujeito fica suspenso, perdido, apagado num conjunto aberto de significantes encadeados. Somos o sujeito do ato e com esse ato, no entanto, desaparecemos. Somos o sujeito do ato e não somos (4). Aqui está o que se poderia chamar de antinomia do sujeito.

II – Nós podemos, em primeiro lugar, representar essa antinomia mediante um objeto topológico introduzido já faz um bom tempo na teoria lacaniana. No lugar de definir o sujeito, a banda de Moebius o mostra. Mas seria falso identificar diretamente o sujeito com a banda e dizer assinalando-a: aqui está (5) o sujeito. Não. O que nos interessa na banda de Moebius é que sua propriedade de ter uma só borda muda se se opera um corte mediano (ao menos é o caso de uma fita torcida com só uma meia-torção). Neste momento, quer dizer, no momento de realizar uma curva fechada (que se une a seu ponto de partida), a banda propriamente dita desaparece, e disso resulta uma fita que já não é mais uma banda moebiana. Portanto, não é suficiente representar o sujeito no espaço, faz falta também o ato de cortar, de traçar uma curva fechada. O ato de dizer é do mesmo tipo, já que o significante determina, fende o sujeito em dois, o representa e o faz desaparecer.

Vamos a uma segunda maneira - lógica, desta vez - de considerar a antinomia. Para fazê-lo, retomemos a análise, estabelecida desde longa data pelo discurso lacaniano, da relação entre o Um e o zero em correspondência à relação entre o sujeito e o significante.

Eu não vou entrar em detalhes da demonstração, que foi rigorosamente tratada por J. A. Miller em seu texto sobre "A Sutura" (6). Vou me limitar aos pontos essenciais dessa correlação a fim de responder à questão que nos preocupa: como dar conta desse fato teórico de que o sujeito é impossível e no entanto nomeado, e mais que nomeado, contado como um (seja um a mais ou um a menos)? Como esta coisa fugaz que é o sujeito pode ser fixada como um significante?
A aproximação com a definição de zero fornecida por Frege é aqui esclarecedora: é um número dotado de duas propriedades: por um lado ele designa o conceito de um objeto impossível, não como referência à realidade, mas à verdade, porque não idêntico a si e, por outro lado - em relação à sequência dos números - o zero conta como um. O zero se define, então, enquanto conceito do impossível e enquanto elemento que ocupa um lugar na sucessão numérica. Da mesma forma o sujeito, ao mesmo tempo em que é rejeitado pela cadeia significante, permanece no entanto representado por um significante e, portanto, elemento contável.

Portanto, há uma estreita afinidade entre o sujeito e o zero, ainda mais íntima e importante se se considerar esta função que lhes é comum: tanto um quanto o outro asseguram, por seu lugar singular, o movimento da série de números. Assim, quando definimos o sujeito do inconsciente como efeito do significante no ser falante, queremos dizer que o desfile do significantes através de nós faz de nós uma constante, um zero, uma falta, um pilar faltoso que vai precisamente sustentar a cadeia.
Como tudo isso é jogado na análise? Não é uma especulação descarnada? Que outro objetivo analítico podemos esperar, se não for o de que o sujeito, em uma análise, fale, não para dizer sentidos, para significar, mas para se significar? Quer dizer que um sujeito fala - aí reside o paradoxo - para desaparecer, para que faça ato e se apague em seguida. Solicitamos, esperamos que o sujeito se demita, venha ao Outro, desapareça e, simultaneamente, volte a lançar a cadeia dos significantes inconscientes. O sujeito diz e, dizendo, advém como sujeito (espaço em branco) (7) e desaparece. Antes do ato não era, depois do ato não é mais. O sujeito "ex-siste fora dessa cadeia, mas em relação a ela. (8)

Neste ponto da demonstração, antes de entrar no problema da castração, já antecipando a interrogação que eu gostaria de compartilhar com vocês: porque, se todo o sistema é significante, se a ordem é significante, introduzir aí o termo sujeito? Porque Lacan tende a guardar esse termo lá onde, em princípio, tudo conduz a dizer que não há nada disso? Ora, já está claro que negar a existência do sujeito, ao menos desde o ponto de vista da teoria lacaniana, é um erro. Se vocês dizem: o sujeito está sob o significante, logo não está, cometem um erro. O sujeito está dividido, assim está na cadeia. Lacan insiste em conservar esse termo de sujeito, quer dizer a utilizá-lo, para diferenciar a psicanálise do formalismo.

Mesmo em relação a Freud, ele mantem o sujeito. Há uma citação muito bela, falando de satisfação do desejo (vocês sabem que o desejo se satisfaz no símbolo, no significante)) Lacan afirma: "Freud nos disse: `o desejo se satisfaz`, enquanto proponho: o sujeito (9) do desejo se satisfaz". Porque não desiste dessa questão do sujeito?

Retomando este desvio, esta nuance em relação a Freud esse desvio, esta nuance em relação a Freud, podemos indagar se é o conceito de satisfação que o leva a não abandonar o sujeito. Será necessário invocar o sujeito para falar de gozo ou satisfação? A meu ver, não é este o caminho a seguir, vocês verão mais tarde que a relação entre sujeito e o gozo é uma relação de oposição. Se poderia dizer com algumas reservas: lá onde há gozo, não há sujeito. Não é, pois, esta problemática do gozo que explica sua ligação ao conceito de sujeito.

III - Antes de expor qual é a problemática que este termo, sujeito, vai resolver, vejamos nossa terceira relação, aquela entre o sujeito e a castração.

É no quadro da castração que encontramos em Lacan uma primeira resposta, inspirada pelo termo de afânise extraído de Jones, ao qual ele se refere na maioria de seus Seminários para fazer - não sem admiração - a sua crítica. Nesse sentido. Além disso, certos conceitos importantes na teoria lacaniana são tão fortemente marcados por Jones, que disse a mim mesmo que Lacan ama Freud como seu duplo, mas é a Jones que ele deseja.
Assim, quando Freud escreve: o desejo se satisfaz, ele diz: o sujeito do desejo se satisfaz. Jones propõe: afânise do desejo, ele diz: não, afânise do sujeito. Então ele encontrou uma maneira de dizer: não é que o sujeito esteja ausente da cadeia de significantes, não é que não estejamos nos mil e um acontecimentos que vão se suceder, é que o sujeito está, mas como que apagado, o sujeito "se afanisa", se desvanece no Outro.

Se agora nos referirmos à castração e à distinção estabelecida por Lacan já há vários anos, ente ter o falo e sê-lo, veremos este conceito de afânise desdobrar-se segundo o lugar que o sujeito ocupa em referência ao significante ou ao objeto fálico.
Eu não posso entrar aqui no exame aprofundado de um ponto que tratamos alhures. Perguntemo-nos simplesmente, à título de lembrete, o que queremos dizer quando utilizamos a expressão bem conhecida "ser castrado"? Nós colocamos aí três significações. Inicialmente, que o ser se confronta com o sexo por dois meios, o significante (sintoma ou não) e o fantasma, meios artesanais, incapazes de resolver o impasse do gozo entendido aqui como inexistência da relação sexual. Em seguida, que o recurso aos significantes é um constrangimento e uma submissão: constrangimento a uma repetição inútil, pois a suplência não se realiza, ela falha, e submissão ao termo que ordena essa repetição: o significante fálico. Ter o falo quer dizer isso, não ter absolutamente nada e continuar, no entanto, submetido à função fálica. E, enfim, que, neste trabalho inexorável de revelação de significantes uns após os outros no curso de uma vida, o sujeito se extingue passivamente, se "afanisa". Aí está uma das forma de desaparecimento.

A outra forma, relativa a ser o falo, depende de uma dimensão bem diferente, a do fantasma, onde vemos desaparecer o sujeito escondido por trás do objeto fantasmático. É preciso, assim, sumariamente distinguir duas classes de afânise, duas maneiras de não estar mais ali (o que é totalmente diferente de não ser): uma maneira própria à repetição, outra própria à ocultação.

Se vê, então, sem dificuldade, que a castração não é uma operação negativa de eliminação de um órgão. Ao contrário, é um trabalho de proliferação inexorável de significantes sucessivos. E, se qualquer coisa é afetada pela privação, não é o pênis, é o próprio sujeito. Castrar é decapitar, pois quanto mais os significantes insistem e se repetem, mais o sujeito é reduzido. Se agora, para resumir, nós mudamos de vocabulário e nos perguntarmos novamente o que é a castração, diremos que ela é uma iniciação, uma entrada da criança no mundo do fracasso em abordar o gozo (nem mesmo para conhece-lo, mas somente para significá-lo), ao preço do desaparecimento. Uma vez mais, chegamos à mesma conclusão: a criança entre no mundo e empalidece.
Retornemos à interrogação de há pouco: de que tipo de obstáculo o termo sujeito nos liberta? Submeto à apreciação de vocês a ideia de que o impasse levantado por Lacan é a alternativa já muito antiga entre o ser e o não-ser. Lhe era necessário - em minha interpretação - não ontologizar o sujeito, não fazer dele um substrato, lhe era necessário, dito de outro modo, não atá-lo à noção de representado. Lhe era necessário que o sujeito não fosse somente uma coisa marcada pela representação, aquilo que para Berkeley se traduzia por sua célebre fórmula: "o ser é o ser percebido" e, para nós, por "o sujeito é o sujeito representado".

Trata-se, pois, para Lacan, de evitar esse sujeito substrato, identificado exclusivamente a uma representação. Se o sujeito fosse apenas isso, pura representação, seríamos naturalmente conduzidos a erigi-lo em entidade absoluta, substancial. Ora, era necessário, para não acabar no filão da metafísica, que o sujeito fosse outro.

Lacan, assim, guarda numa mão essa noção de representado mas, para que isso não seja um substrato, introduz então, com a outra, a noção de sujeito apagado em toda a cadeia. A recíproca é verdadeira: a necessidade de não fazer desaparecer completamente o sujeito explica o recurso à noção de sujeito representado. Essa dupla mão, certamente, é o sujeito dividido. Quero ser claro sobre esse ponto: a astúcia não consiste tanto em ter dividido o sujeito - ele poderia tê-lo dividido em ser e não-ser - quanto em tê-lo dividido entre a representação e o conjunto das representações. Que interesse tem isso? É que, desse modo, ele divide o sujeito entre ser representado e, por outro lado, o faz brilhar em tantos ditos, em tantos significantes quantos se ordenam em cadeia. Assim, ele guarda o sujeito e conserva, sobretudo, a cadeia: a cadeia de representações inconscientes ou a cadeia de significantes. Insisto ainda no fato de que a divisão do sujeito não é feita entre ser e não-ser, mas entre o um e o Outro, entre um significante que o representa e o desvanecimento na cadeia, ou ainda, para retomar nossas letras, entre S1 e S2 (10).

Ora, a solução de dividir o sujeito elidindo esses dois riscos repousa inteiramente sobre a função representativa: um significante representa o sujeito para um outro significante. Sem esse conceito de representação, a divisão do sujeito seria impensável, pois é por um significante que o sujeito se mantem ligado ao sistema de representações. Mas - aí está a interrogação que fiz ao Sr. Lacan e que submeto a vocês - esta amarra da representação não será muito frágil para manter unidas duas dimensões tão heterogêneas: a determinação significante e o efeito de um sujeito desaparecido? Como conceber que a representação possa reunir a determinação e o dejeto, a causa da abolição e aquilo que é abolido? Para alguns de vocês uma tal questão pode suscitar objeções, entre as quais algumas já poderiam inclusive encontrar na trama desta exposição e inclusive ser formuladas por mim mesmo. Entretanto, prefiro, ao contrário, não fazer calar a questão e deixar que ela nos conduza, mesmo que sejamos mais tarde obrigados a voltar sobre nossos passos.

Assim, a partir desse questionamento da representação enquanto divisor do sujeito, me parece possível, ao invés de divisor horizontalmente o sujeito, multiplicá-lo verticalmente em tantos significantes que componham uma cadeia. Um sujeito escalonado, em folhetos, em suma. Essa concepção espacial do sujeito nos surgiu com a consideração de uma certa classe de superfície topológica nomeada de Riemann (11), definida por uma função analítica. Riemann, sábio e matemático do século XIX, resolveu genialmente - no quadro da teoria das funções analíticas de variável complexa - o caso anormal de uma função multiforme. É o caso - que apenas menciono - de uma variável (relativa a um número complexo, por exemplo, a raiz quadrada de z) à qual corresponde mais de uma função. A fim de superar o obstáculo de uma irregularidade embaraçosa para outros cálculo (cálculo integral), Riemann sai, por assim dizer, do campo próprio das funções algébricas e recorre ao espaço geométrico, até mesmo ao imaginário do espeço. Assim, ele procede a uma multiplicação da variável por tantos valores quanto forem as funções. Portanto, ao invés de procurar reduzir o número de funções e atribuir uma função a uma variável, ele encontra este mesmo acordo decompondo o valor da variável, em uma palavra, ao invés de diminui as funções ele multiplica as variáveis (12). Ora, esta multiplicação terá, ao menos no percurso de Riemann (isso foi modificado depois), um suporte espacial, topológico. Ele faz uma construção composta de folhetos superpostos, cada um deles correspondendo a um valor, e o conjunto recobrindo o plano dos números complexos. O número de estágios ou de folhetos pode, conforme o gênero de superfície, subir ao infinito. É esta estrutura, precisamente, que se denomina de Riemann.

A analogia de uma análise desse tipo com o sujeito é, para nós, notável. Porque não supor - ainda que devamos nos corrigir depois - que o sujeito se submeta ao mesmo acréscimo, ao mesmo folhetear a que Riemann submetia o valor da variável, e supor, ainda, que se o sujeito se multiplica assim na medida dos significantes que compõe a cadeia, termina por se identificar a ela?
Nós sabemos bem que isso significaria liberar o sujeito de toda ligação ao sistema, já que ele se torna esse sistema. Nós sabemos também que existe um nome para designar essa assimilação do sujeito pela cadeia, o sujeito suposto saber. Nós sabemos ainda, como eu tentei explicar, que não se deve confundir negação do sujeito com dependência do sujeito, que uma coisa é dizer que o sujeito não é, e outra que ele se afanisa. Tudo isso, nós sabemos. Mas ordinariamente, quando os psicanalistas que somos praticam tanto a teoria quanto a análise, este sujeito escorre entre nossos dedos. Raciocinamos e filosofamos como se, de fato, o termo sujeito não fosse mais que um ornamento a mais, um "joker" (13) cômodo no nosso jogo teórico. Tudo se passa como se fossemos "sujeitistas" no pensamento, mas formalistas no coração.

Ora, quando propomos (14), com o apoio da superfície de Riemann, ver o sujeito se folhear e desaparecer, estamos levando ao extremo esta intuição que negligencia o sujeito. Ou melhor, talvez o estejamos interrogando como um sintoma, em lugar de tentar obstinadamente corrigi-lo. O terreno estaria, então, mais livre para se reconhecer facilmente a necessidade de aprofundar a afânise efetiva do sujeito e, ao mesmo tempo, em consequência, reelaborar a dimensão imaginária do eu (15). A partir de nossas formulações sobre o sujeito é, particularmente, este tema do eu e da intuição que se oferece ao exame. Se o sujeito resta confinado à cadeia, como nós o supomos, se impõe, então, a necessidade de nos debruçarmos sobre a importância da instancia imaginária do eu e analisar mais fundo sua relação com a intuição.
Em suma, trata-se de manter viva a questão: "quem é o sujeito"? Se retomarmos nossa terminologia falando de castração, se, em lugar de sujeito, dissermos a criança, se ao invés de cadeia utilizarmos lei do pai, se ao invés de afirmar simplesmente gozo (16), acrescentarmos gozo da mãe e, enfim, nos perguntarmos quem é essa criança magnífica de quem a psicanálise tanto fala para sustentar suas hipóteses, deveremos, então, responder que esta criança, esse sujeito, portanto, é aquele que fala e pensa com palavras do pai atraídas pelo gozo da mãe. É a criança que não sabe o que é dito e sequer pode gozar. A criança magnífica da psicanálise, nós, os seres falantes, somos apenas seres de vento, mensageiros que se desvanecem entre o gozo que aspira as palavras e o nome do pai que as ordena (17).

Vappereau: – Eu não queria interromper Nasio no momento em que ele falava da banda de Moebius, porque creio que, como com o espaço de Riemann, imaginamos que é partir dali que poderíamos dialogar. Então, vou a desenhar essa banda de Moebius e vocês encontraram o comentário do desenho que vou fazer em O Aturdito, que se encontra em Scilicet. Eu não tenho a intenção de ilustrar este texto e eu vou usá-lo apenas para responder a pergunta ... enfim, digamos, o Doutor Lacan me incitou a lhes falar, ele me presenteou com os quatro volumes do Seminário que foram editados e me pediu que tirasse alguma coisa deles para vocês e eu fiz alguns desenhos.

Então, aqui está a banda de Moebius da qual nos falou Nasio a propósito do S1----> S2 em termos de matemas, e vou traçar o desenho do corte do qual ele nos falou de uma maneira brilhante. Aqui está o corte.

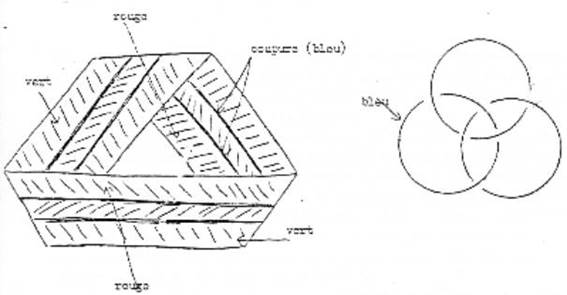
Se vocês extraem a aba da superfície que obtém, logo depois do corte, de acordo com o traço azul, que é um traço contínuo, vocês obtém uma superfície com uma só borda e uma só face, que é, ela mesma, uma superfície de Moebius.
E do outro lado do quadro, vou desenhar isso no outro extremo, uma cadeia borromeana na qual vou também colocar uma das consistências em azul. Então, aqui está. É entre esses dois desenhos que vou tentar lhes falar dos quatro volumes do Seminário, a propósito de dois termos, a propósito, primeiramente, do termo de máquina à partir desse nó.

Assim, nestes quatro volumes, as máquinas ocupam um lugar muito importante, no segundo livro, no livro II. E é bem evidente que, quando comecei a ler o livro I, dado que apareceu ao mesmo tempo que Mais, Ainda, o livro XX - o livro XX, eu havia assistido o Seminário, estava muito contente assim, de tê-lo, para poder lê-lo - e bem, o livro I, devo dizer que não compreendia muito bem o começo, onde estava a questão do ego (18), um termo que não conheço já que não é, digamos, um assunto no lugar de onde venho, então, esperei um pouco, e é somente a propósito dessa questão para mais além da psicologia que me encontro particularmente interessado.
Ora, essa questão é desenvolvida no Seminário nos termos de Imaginário e Simbólico que, num primeiro tempo, lhes proponho considerar como sendo as duas faces de uma banda bipartida, que estão aqui, de um e de outro lado do azul, já que seria necessário que se dessem conta que, sendo desenhando-a, seja cortando-a, se obtém - sobre a banda de Moebius assim - se obtém uma banda bipartida, quer dizer que se separa a banda, não em duas partes - não importa quais - senão em duas faces. Eu vou colori-las: aqui uma verde, aqui uma torção, então há o outro lado, mas o verde reaparece aqui novamente aqui e segue verde se continuo. Aqui é o outro lado e aí está o verde que reaparece. E em seguida há uma parte que colori em vermelho que é o avesso do verde.

Então é a propósito dessa banda que me propus ficar o mais perto possível do Livro I do Seminário e que pude me dar conta que a parte que corresponde ao azul era o Real. Então, no fim das contas, há muita inabilidade de minha parte em apresentar as coisas assim, porque é francamente uma representação. Mas no Seminário, Livro I se encontra o que efetivamente é uma questão do Real sobre, me parece, a Verneinung de Freud, comentada por Hyppolite e é assim que a conectei com a expressão de Madame Lefort sobre esses dois termos: "O lobo! o lobo!" (19).

Bem, mas, em seguida, voltemos às maquinas. O Seminário seguinte, o Livro II, desenvolve, me parece, esta questão das máquinas e que me causou muita supressa voltar a encontrar esse aspecto, na medida em que as havia estudado como autômatos abstratos com os matemáticos e, assim, havia feito uma ideia do que uma máquina poderia ser, embora não se pense muito frequentemente que uma polia ou um dado sejam máquinas. E o que eu quero é falar de máquinas que são um pouquinho diferentes umas das outras, e falar do nó e das cadeias como máquinas.

Então, se me atenho neste momento à época desse Livro II do Seminário do Doutor Lacan, se me atenho às máquinas matemáticas, as máquinas recursivas que produzem uma repetição de uma operação por tanto tempo quanto se queira, que têm limitações e que fracassaram em dar conta das linguagens naturais, bem, essas máquinas tem uma cabeça de leitura ou de escritura, e bem, creio que não é necessário se preocupar excessivamente da cabeça ou unicamente (20).

Os matemáticos e os lógicos, o problema que que se fizeram com essa cabeça, é o de saber se ela passava a diferentes estados. Se chama a isso os estados da máquina e se anota S1, S2, etc... Ora, isso me serviu muito como analogia, a princípio, para seguir o programa, a gramática dessa cabeça. Mas muito rapidamente fui conduzido a desdobrar essa cabeça e, agora, me dou conta perfeitamente que aquilo que há frente a cabeça é o que se chama banda-máquina, me dou conta absolutamente que é necessário se ocupar da banda. Somente as bandas nas máquinas de Moebius, não precisamente de Moebius mas de Turing, não tem torção, quer dizer que são máquinas que são forçosamente lineares e, com essas máquinas, jamais se chega a se fazer (21) outra coisa do que elas sabem fazer, mas logo se encontram restrições, um limite, quer dizer que o limite se encontra do lado do infinito, quer dizer que é necessário emendar para dar conta das linguagens naturais, ao que parece, uma infinidade de máquinas, umas ao lado de outras, para conseguir fazer o quê? Alguém poderia perguntar, mas do lado da banda, que interesse há pela banda como máquina, e é já uma etapa como aquela que desenhei ali. E vocês veem bem que não é suficiente mostrar isso com um só desenho, é necessário transformar, é necessário fazer funcionar essa máquina. É, assim, uma etapa das máquinas.

E me parece que com isso já se poderia fazer algumas coisas. Então, como me interesso seriamente por essa banda com suas torções e seus furos, vou desenhar outra apresentação dessa banda com um furo, e lhes mostrar uma pequena maquinação bastante surpreendente, mas, enfim, antes os dois termos, já que é demorado fazer os desenhos intermediários e é todo um exercício.
Então, antes, se trata dessa banda sobre a qual abro um furo. Se abro um furo aqui e estendo esse furo até prolongar as bordas desse furo, obtenho aquele. Vou desenhá-lo aqui de um modo bastante grosseiro, quer dizer, que faço na borda do furo um furo do furo central, e volto a colocar a parte azul. Aqui está!

Bem, essa figura, sobre a qual é possível ver o vermelho e o verde, se verifica que essa figura é o que se chama de banda encruzilhada. E com a banda encruzilhada, se se corta a parte azul que já colori, se obterá uma banda encruzilhada duas vezes fendida e que vou arrumar. Então, objetos que desenho têm propriedades e se descobre que, quando leio, eu tento tirar todas as figuras de uma série de objetos que já desenhei, tento tirar e ver se o que leio oferece alguma coisa, responde ou ressoa com os desenhos e os problemas que são aqui problemas de superfície. Ora, isso não funciona jamais por um longo tempo, isso, eu creio que é uma constante, uma constante dessa forma de fazer que é que se chega a cada vez a um momento em que as coisas parecem insuficientes.

Mas o que eu gostaria de tentar dizer é que há um salto, uma vez que a outra máquina já começou a funcionar quando se abandona um certo tipo de máquina. E não é necessário começou a marchar outra máquina quando se deixa um certo tipo de máquina. E não é necessário procurar levá-las ao extremo, quer dizer ao extremo, quer dizer à nenhuma parte. Por exemplo, vou lhes mostrar sobre essa figura, está ali já o desenho das bordas e eu posso me interessar pelas bordas. Ora, o que é que essas bordas vão me dar? (22)

E bem, vejo aqui que há um furo. Ora, o buraco, se pensamos sobre o buraco o raciocínio sobre o furo, se pode não imaginar muito bem que ele é independente, totalmente independente das outras bordas que estão sobre essa superfície, já que se vê bem aqui que é independente da parte azul e da outra borda exterior vermelha. Aqui podemos ver que a borda desse furo negro é totalmente independente. Essa pequena pastilha não está enodada. Em consequência, posso em troca desenhar a parte azul e a parte vermelha, a parte azul, isso fará um oito interior sobre o qual vem a enodar-se, em vermelho uma consistência, a parte azul, é a borda da banda de Moebius que está traçada sobre a banda de Moebius e a borda do furo é o círculo negro.
Então, eu então fazer assim monstração de um caminho que fracassa e recomeça sucessivamente... No Livro II, que fala da questão de máquinas, a propósito do Seminário, tentei aplicar essa máquina, quer dizer, esta, esta banda encruzilhada, ao sonho que Freud tem sobre Irma e de onde parte o Dr. Lacan. Então, efetivamente situo o movimento do sonho e me dou conta que efetivamente no comentário se pode seguir muito precisamente a Freud, que se afasta, que fica de lado com Irma. Então ele parte, em lugar de restar sobre a banda, que é atravessada pela parte azul, se projeta aqui (esquema II), quer dizer que na encruzilhada se aparta do trajeto normal da banda azul. E vocês veem que ele será conduzido para passar sob a banda. Ora, é nesse momento que ele vê a boca aberta de Irma, e a observação que foi feita no Seminário foi que, nesse momento, ele teve que acordar, ora, mas ele não acorda. Então, qual foi a minha questão? Me disse: o que é que faz com que ele não desperte? E trabalhando essa bandas, por um lado, e sonhando também, cheguei a situar o despertar do lado da torção, quer dizer que parecia que, nesse desenho, Freud não encontrou torção.

Então, o que eu queria lhes mostrar era de que maneira, se se corta essa banda que vou terminar de colorir segundo suas três bordas, se se corta essa banda, se pode conseguir apresentá-la assim, se pode apresentá-la assim, sem torção.

Quer dizer que vocês imaginam a complexidade para mostrar isso diretamente por transformações contínuas. Então aí é preciso fazer um pouquinho de matemática. O que entendo por fazer matemática neste momento é buscar meios intermediários que me permitam justificar essa transformação que encontrei, já que eu trabalhava com esses objetos.

Então, hachuro a banda plenamente, já não há mais torção e se trata de uma verdadeira espiral. Ora, me parece, em consequência, que tudo isso tem muito a ver com os problemas da análise, quer dizer que essa espiral sem torção, digo, de imediato, que não creio que seja uma psicose, eu diria que isso tem alguma coisa que é da ordem da análise, é um primeiro esquema que encontrei, bastante evocador, no Livro I do Seminário, durante a última reunião em que o Dr. Lacan nos propôs um esquema da análise que data dessa época do Livro I do Seminário.

Então vocês vem a questão que se elabora, é que há uma parte de ilustração e há uma parte matemática que preservo e que, na minha opinião, não é indispensável desenvolver de outra maneira, e vou tentar me explicar sobre isso falando justamente do Livro XI que, ele, retoma, na minha opinião, enfim, tal como o li, o Livro I. Me pareceu que era um desenvolvimento análogo, ora, é uma questão que esse Livro XI, cheio de matemas, de escrituras matemáticas que correspondem pois, à uma outra ordem que aquilo de que Nasio falava à pouco, que não é topológico, mas que fala imediatamente de lógica com o zero de Frege, essas coisas efetivamente estão muito presentes, essas diferentes forma de abordar uma questão, se se quer se ater a ela, seja com bandas ou seja com escrituras. E é em torno desses termos que nós giramos.

E bem, eu diria que o Livro XI no qual há muitos matemas, que surpreendem os matemáticos que não compreendem nada disso, é necessário ser um pouco lógico para seguir aquilo, e creio que com as cadeias e com os nós se chega particularmente bem a pegar isso.

Então é por isso que vou pular para o Livro XX que, ele, me parece extremamente denso, muito conciso, mas no qual se trata dessa falha compacta, que os matemáticos podem ler e reconhecer como a definição, totalmente correta, do que conhecemos como compacidade, e creio que se pode reenviar essa falha compacta ao que vem de fora, perceber que, por exemplo, ela reenvia ao Seminário XI, se se o lê, no momento em que justamente a rede de significante é apresentada, no capítulo justamente anterior ao que se chama " Inconsciente Freudiano" (23) e onde Lacan, depois de ter falado de Lévi-Strauss e do "Pensamento Selvagem", diz que existe algo um pouco diferente do pensamento mágico, é a descontinuidade (24).

Então isso deve fazer rir, ainda mais aos matemáticos, a descontinuidade nesse momento, já que a topologia se define justamente por funções contínuas. Portanto, isto pode parecer extremamente difícil e não obstante, penso, que nos termos do ensino de Lacan, que se deve desenhar, para evitar, justamente as minhas matemáticas enquanto que prática da escritura, já que os nós e as cadeias, isso aponta justamente para alguma coisa que é necessário diferenciar das superfícies que desenhei aqui, no quadro, as quais são máquinas ainda sumárias em relação as cadeias que são máquinas, eu diria, mais consistentes, que se podem praticar muito simplesmente, assim como os dados são máquinas: se pode fazer rolar os dados, se pode também lançar as cadeias borromeanas, borromeanas ou não, por terra, e recolhê-las, retomá-las.

Ora, eu sou da opinião que desenhá-las, quando se chega a desenhá-las, se produz tensões estruturais que podem ser melhor seguidas do que com a manipulação do modelo físico. E se chego a discutir esse termo de modelo, já que, se o evoco nessas máquinas, por um lado e as matemáticas, por outro, é um critério para poder constituir na matemática o que se chama modelos.

E então eu digo que não se trata de modelos já que, finalmente desenho - e aqui eu inclusive desenhei de forma muito desajeitada - mas o proponho justamente devido ao seguinte: não se trata de modelos já que o Dr. Lacan conduziu o trabalho sobre as escrituras dos matemas até o ponto, em Mais, Ainda, de produzirmos alguma coisa - não diz isso nesse Seminário, senão um pouco mais tarde - que alguém já havia assinalado e que se trata, na ocasião, do "não-todo". Ora, efetivamente se se estuda as matemáticas, quer dizer, a questão da teoria das matemáticas, quer dizer a questão da teoria dos modelos, da teoria dos conjuntos na linguagem do cálculo de predicados, não se compreende nada do "não-todo", não se o descobre jamais, já que todo o assunto está feito justamente para o τ (x) (25) de Hilbert e as coisas não apareçam. Em consequência é necessário ter outra ideia do que se busca para encontrar o "não-todo" na teoria dos conjuntos e no cálculo de predicados. Mas está perfeitamente articulado e é com esse argumento que se chaga a produzir alguma coisa. Ora, digo que depois, no Seminário XX, depois de ter articulado precisamente, sobre o matema, o limite final do qual o matemático faz o cálculo de predicados e que não está obrigado a pular, bem, se encontram as cadeias, quer dizer, se retorna às máquinas, se deixa esses modelos e a teoria dos conjuntos, inclusive mais mecanizadas, e se volta às máquinas muito mais simples. E são essas máquinas muito mais simples as que me parecem interessantes de serem praticadas.

Então eu diria: o que é que há de particular com essa cadeias, para terminar? Para retomar a questão de Nasio, junto com a questão do Um e do Outro, eu diria, para responder também a essa questão da representação da representação ou do Nada que, se traço uma cadeia de quatro, se traço uma cadeia borromeana de quatro, bem, há três anéis - e isso, o Dr. Lacan disse muito bem nos Seminários que apareceram na Ornicar? (26) - há três anéis que vou desenhar, um em azul com a figura anterior, quer dizer, esta aqui, outro em vermelho e um terceiro em verde.

Se cortamos um dos três que estão coloridos, o quarto sendo este negro, os outros dois ficam livres, pois estão enodados.... eles apresentam alguma analogia com a estrutura borromeana, quer dizer, se se corta um dos três, qualquer um dos três, os outros ficam livres. Ora, o que se passa com a estrutura borromeana? É que o quarto está implícito, disse Lacan em alguma parte, ao longo dos Seminários seguintes, quarto está implícito, e bem, a questão é saber o que sustenta os três.

Cada um dos três sustenta aos três, cada um dos três sustenta aos outros dois, podemos dizer, mas se pode inclusive dizer que sustenta aos três. Mas nada - mas então se cai na mística? - nada, mas é um nada que conta, quer dizer, um vazio, já que não é uma questão representá-lo aqui por um quarto. Aqui, eu diria que o quarto está explícito. Aqui o quarto está explícito, eu o nomeio Σ, aqui quem é que sustenta os três? É a estrutura borromeana quem faz isso, quem, os sustenta, é um nada que conta.
Aqui está, como eu diria, que esse efeito de nodalidade - aqui está como o vejo e como o digo - esse efeito de nodalidade permite, eu acho, fazer jogar alguma coisa que não é representável e que não pode ser esgotado por nenhuma máquina, quer dizer que é uma máquina, mas em contrapartida é uma máquina em si mesma que se pratica, quer dizer que está ao alcance da mão e que é, eu acho, alguma coisa como, para evocar a passagem no Seminário em que, pela primeira vez aparece a nodalidade, é alguma coisa como tiro ao alvo (o terceiro esquema, acima), quer dizer - tomo essa referência do Livro XI onde Lacan apresentou a pulsão nesse termos, fazendo esse desenho a propósito de uma borda - e bem, é o circuito de ida e volta da pulsão que contorna o a.

É a primeira ocorrência da nodalidade nos desenho do Dr. Lacan. Observem de que maneira fiquei surpreso ao encontrar outro desenho que, em si, nunca é comentado, que apresenta exatamente essa borda e esse circuito.
Aqui ainda se trata de uma cadeia de três com uma consistência que passa por um furo, enfim, que considero como um furo, e que é uma cadeia borromeana. Ora, devo dizer que o recurso à essas figuras, a questão que me faço é, a propósito justamente da ideia de ensinar ou de poder discutir isso é: que tipo exatamente de aplicação é necessária para se conseguir fazer disso alguma coisa? Quer dizer, que me parece que efetivamente ali - eu não tinha me orientado para isso a não ser agora - havia algo que jogava no texto dos Seminários, quer dizer, que o Dr. Lacan escrevia ou falava - e por isso intitularia de bom grado isso de "máquina de escrever", porque isso dá em algo escrito - e bem, falava, digamos, de uma maneira material e consistente. Ele conseguiu desenvolver suas diferentes máquinas até encontrar a cadeia borromeana que agora... que podemos fabricar para quê?

Para funcionar, para funcionar e nesse momento, com essa máquina que, parece, quando a prática dá efeitos, sobretudo assegura, eu diria, uma grande consistência material ao discurso, quer dizer, que ela permite fazer das etapas da leitura como da escritura, por um lado - e isso eu tomo em um sentido muito amplo - ela permite fazer passeios, pequenos percursos maquinais que falham. Mas é exatamente como na interpretação de um dito espirituoso, quer dizer que quando não se esgotou a estrutura, quando se fez funcionar a análise de um dito espirituoso e não se o esgotou, mas que se tem, de um certo modo, a impressão de que foi drenado, deteriorado o brilho dessa lâmpada que é o dito espirituoso. E bem, com a estrutura aqui presentificada, vocês podem fazer funcionar, podem trabalhar as cadeias, mas não a esgotarão jamais, jamais dirão o que é, neste caso, na cadeia à três e, se não se trata de representá-lo, eu não creio que isso seja algo já dado e que faz sustentar as cadeias, vocês se encontrarão confrontados com a materialidade da cadeia.

Portanto, o que me parece importante é que, com o último desses Seminários, quando se alcança a nodalidade, que reconheço como tal, e bem, não é o caso de continuar em um movimento infinito de constituição de máquina, já que ali se encontra uma máquina que não se esgota, me parece, que está no espaço, estruturando o espeço de uma tal maneira que não se esgota e não pode esgotar o espaço.
Então, em todas as etapas precedentes, era essa estrutura que refletia, que fazia saltar as diferentes máquinas e que era necessário fazer funcionar. E o que isso nos ensina é que é necessário fazê-las marchar, quer dizer, que não se trata simplesmente de observar para aprender alguma coisa.

Então, do lado da escritura matemática, eu, devo dizer, que a pratiquei muito cabalisticamente à ponto de ler Bourbaki, quer dizer, para terminar, eu diria que há uma torção nos escritos matemáticos muito difícil, me parece que os espaços laminados aos quais você fazia referência, são muito difíceis, são inclusive inimagináveis, mas não creio que se tenha uma garantia melhor da estrutura.
Do lado de uma coisa que pode ser matematicamente inscrita no cálculo de predicados, se se lê a questão do "não-todo" tal como Lacan a articula no Seminário Mais, Ainda, se vê que inclusive sobre o cálculo de predicados - aí está a questão do modelo - os espaços laminados, não é necessário recair neles enquanto modelo.

(1) Esta intervenção pode também ser encontrada, com ligeiras diferenças, com vários acréscimos e com algumas supressões – lá e cá – no ótimo livro A Criança Magnífica da Psicanálise – O conceito de sujeito e objeto na teoria de Jacques Lacan, publicado por Juan David Nasio pela Jorge Zahar Editor.

(2) No texto francês está Fregge, mas o nome do matemático a quem se refere tanto Lacan como Juan David Nasio é Johann Gottlob Frege.

(3) Exatamente assim em nossos textos base.

(4) Nesse ponto há uma nota que replicamos tal qual: Eu pronuncio "nós somos". Ora, logo depois percebemos que "nós somos" é uma inexatidão. Porque se eu digo que o sujeito está no ato, em seguida ele se apaga em todos os ditos que se sucedem, e fica a questão: mas o que é esse "nós”? Digo " nós somos", pois de que modo indicar de outra forma que "não saberíamos especular sobre o sujeito sem partir disto: que nós mesmos, como sujeitos, nós somos implicados nessa profunda duplicidade do sujeito?" (Lacan). (Esse último ponto de interrogação não consta no texto francês).

(5) “voici” está sublinhado em nossos textos base.

(6) Há no texto francês, aqui, um ponto de interrogação. Sem dúvida nenhuma se trata de um erro de digitação pois remete, antes de mais nada, a uma nota que indica onde está esse texto de Jacques Alain-Miller, ou seja, em “Cahier pour l'analyse “; n° 1-2, p.39-51, Paris, 1966.

(7) Assim mesmo, no original.

(8) No texto francês há, depois do término desse parágrafo, um ponto de interrogação entre parênteses que não se conecta a nada.

(9) “sujet” está sublinhado, no original.

(10) Há um entre parênteses aqui que enfatiza que se trata de S índice 1 e S índice 2. Talvez porque S1 seja homofônico a essain, enxame, em francês.

(11) Nos textos que tomamos como base há uma nota, que está assim: A superfície de Riemann ou estrutura de variedade analítica complexa é uma das fontes comuns da teoria das funções algébricas e da topologia. Uma de suas propriedades, que pode nos interessar particularmente no manejo dos objetos topológicos introduzidos por Lacan, é a orientabilidade da superfície de Riemann. Inversamente, toda superfície fechada orientável é homeomorfa a uma superfície de Riemann, é o caso da esfera, do toro e do toro furado (à p furo). Para essa última observação, se pode consultar sem muita dificuldade o II capítulo de G. SPRINGER. Introduction to RIEMANN surfaces, Reading, 1951.
Para os curiosos de plantão, oferecemos, aqui, uma representação possível desta superfície de Riemann (que não consta no original):

(12) Há mais uma nota neste ponto e que reproduzimos aqui: É interessante notar que esta descoberta de Riemann está em estrita dependência com sua teoria das multiplicidades (muito marcada pela filosofia de Herbart). Cf. l'ouvrage de B.RUSSEL, Fondements de la Géométrie, Gautier-Villars, 1901.

(13) Em inglês, no original.

(14) Há um espaço entre “proposons” e “avec”, provavelmente fruto de um erro de digitação.

(15) Como em francês existem duas maneiras de dizer eu, e como Lacan faz usos diferentes desses eus, nos pareceu importante marcar que aqui se trata de “moi”. O mesmo vale para os eu subsequentes.

(16) O texto indica que aqui há um nome ilegível, que aparece na margem direita do documento, e que termina com ..Y, .AY?

(17) O seminário que tomamos como base para a tradução indica, ao final da fala de Nasio, o seguinte: “Este texto foi revisto pelo Sr. J. D. Nasio”.

(18) Assim mesmo, no original.

(19) Depois da serenidade e coerência, revista, por Nasio, voltamos aos tempos da algaravia, na voz de Vappereau.

(20) Parece faltar aqui, como em outros tantos trechos dessa fala, uma continuação, uma palavra a mais. Procuramos não ceder à tentação de oferecê-la aqui para que o leitor sinta na pele o que de fato foi dito ou não dito nesse seminário sobre A Topologia e o Tempo.

(21) Esse significante, “faire”, se repete aqui, no original.

(23) Há, exatamente nesse ponto, uma diferença notável entre as versões gaogoa e de Patrick Valas. A primeira, que foi a mais utilizada nessa tradução, o parágrafo termina com: “Ora, o que é que essas bordas vão me dar?”. Na de Valas, contudo, há uma continuação: “Elas querem me dar uma cadeia. E como é a cadeia das bordas de uma superfície?”. Ambas e às suas maneiras, engatam então em: “E bem, vejo aqui que há um furo” e o texto continua.

(24) O nome, inteiro desse capítulo é O Inconsciente Freudiano e o Nosso.

(25) Esse parágrafo é, no original, um bloco compacto (24 linhas) que resolvemos fragmentar para dissipar, um pouco, as brumas que o envolvem.

(26) A versão francesa não quis correr riscos e grafou tau (x).

(27) Trata-se da revista da EFP, que faz, em seu título, a união de três conjunções coordenativas, típicas do ensino da língua francesa, para melhor apreensão da gramática. OR:conjunção de oposição (alternativa); NI: conjunção de negação; CAR: conjunção de causa.

(28) http://gaogoa.free.fr/Seminaires_HTML/26-TT/L15051979.htm
http://www.valas.fr/IMG/pdf/1979-05-15.pdf
http://www.valas.fr/IMG/mp3/1979-05-15_La_topologie_et_le_temps_10.mp3