 |
|
|
Tradução, organização e notas de Frederico Denez e Gustavo Capobianco Volaco
Aula 1
21 de Novembro de 1978
Há uma correspondência entre a topologia e a prática. Essa correspondência consiste nos tempos. A topologia resiste, é nisso que a correspondência existe.
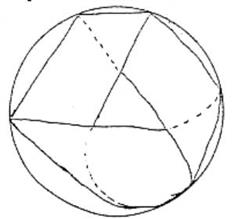
Há uma banda de Moebius que já fizemos seu traçado (1). É o que se chama uma banda tripla. Se pode assinalar que essa banda tripla, o que a caracteriza, é que ela tem bordas, e que suas bordas são quase como isto (2):
(1)
- (2)
Sua bordas são assim, para dizer melhor, assim:
:
Se vocês dobram essas bordas, obtêm algo que se parece com isso:
E o círculo negro toma então esse aspecto. Isso é aproximadamente o que acontece. E aqui o círculo negro é branco.(Lacan mostra uma montagem feita com um anel de cordão branco passando pelo interior de um enrolamento de cordão amarelo)
Aqui está, lhes faço o passo. Há um modo, nessa banda, de cobri-la. Depois disso, isso passa por trás da banda seguinte. Mas o que é preciso ver, é que o que passa por trás da banda seguinte é, precisamente, o que retorna, retorna para frente na banda 3, e depois isso retorna para trás, o que está ali inscrito, quero dizer, por trás da banda tripla de Moebius.
Por essa razão isso retorna à frente. Então o que se tem é:
(1 2).
Na frente (3 4) atrás 6
(5 6)
que junta o 1.Isso é o que eu tenho, da banda envolvente, marcado. Vocês podem manipulá-la e até recobrir a banda tripla.
Aqui vocês tem outro exemplar do que eu chamei por um momento a banda envolvente. Vocês podem constatar a identidade com...
O que é surpreendente é que a banda Moebius normal – e aqui um exemplo – uma banda de Moebius normal, quer dizer uma banda de Moebius assim, tem igualmente o 1 e o 2 e o 3 e o 4 no mesmo lugar. Todos aqueles estão atrás, e estes estão na frente.
E aqui o 1, ele passa aqui por trás do 2 e na frente do 3. No 4, passa por trás, o que permite retornar na frente do 5 e passar por trás para se unir ao 1 que por isso é chamado o 6.
A banda envolvente tem, pois, duas bordas, duas bordas na banda de três, a banda de Moebius de três. O que se vê facilmente na banda que faço circular neste momento.
É um ponto importante. Vocês podem controlá-lo sobre o que faço circular neste momento. Há qualquer coisa em comum entre todas as bandas de Moebius, não seria mais do que essa alternância. É possível - é certo - cortar as bandas de Moebius? Não só se por cortar cada uma, senão que se pode cortar também o que chamo de forro.
O que é o forro? Pode haver um forro só. Mas nesse caso, é necessário cortar a banda de Moebius, a banda de Moebius que é em suma a alma do negócio. Existe uma maneira de traçar sobre um toro uma banda de Moebius. Aqui está como se a traça, se se trata de uma banda de três. Para isso é preciso comprimir o toro e anexar as duas superfícies que são aquelas do toro. A face interior desaparece, é tamponada, esmagada. É também fácil fazer com o toro uma banda de três... o que eu queria dizer, era que é também fácil fazer uma banda de um.
Há, contudo, uma hiância entre a psicanálise e a topologia. E meu esforço, para esta hiância, é de preenchê-la. A topologia é exemplar, ela permite na prática fazer um certo número de metáforas. E existe uma equivalência entre a estrutura e a topologia. É isso, o Isso do qual se trata em Groddeck, é isso o que é Isso.
É necessário se orientar na estrutura. Não há nada como os nós borromeus para isso. Para generalizar o que se chama os nós borromeus, pode haver uma maneira de fazer que não faça que um nó borromeu seja - cortado um - liberado dos outros. E existe uma certa maneira de precisar que, cortando dois sobre cinco, é muito precisamente o que se necessita para que os três restantes fiquem livres. É o que se chama de generalização dos nós borromeus. Cortando dois sobre cinco, os outros três ficam livres. Vou tentar lhes dar um exemplo disso até o fim desse ano.
Muito bem. Eu falei durante uma hora. Obrigado por vossa atenção (2).
Notas
(1)Não tivemos tempo nem paciência para refazer esse e os demais desenhos. Simplesmente os recortamos das versões francesas e os colamos aqui. Mas ficamos, claro, abertos a contribuições.
(2) Ao fim de cada aula indicaremos, como fazemos aqui, as versões francesas que utilizamos para essa tradução:
http://gaogoa.free.fr/Seminaires_HTML/26-TT/L21111978.htm
http://www.valas.fr/IMG/pdf/1978-11-21.pdf
E, logo em seguida, o áudio correspondente:
http://www.valas.fr/IMG/mp3/01_topo21-11-78.mp3