 |
|
|
Mardi 15 mai 1973
On m’a averti ce matin pendant que je travaillais, au dernier moment de mon travail, on m’a averti que le 12 juin, que le 12 juin qui n’est pas, quel que soit le second mardi, qui n’est pas en principe celui auquel j’espérais vous donner rendez-vous, on m’a averti donc que la salle serait occupée par ce qu’ on appelle des examens oraux et que dès lors on pouvait pas me répondre de ceci qu’elle serait libre à telle ou telle heure parce que les examens oraux on ne sait pas comment ça s’étend, comment ça se termine. De toute façon, je n’avais pas l’intention, comme je viens de le dire, de vous donner rendez-vous pour le 12 juin puisque c’est le mardi de la Pentecôte. J’avais par contre l’intention de vous donner rendez-vous le 19 juin, troisième mardi. Le 19 juin les examens continueront, donc je ne peux pas malgré que j’ai élevé quelque objection à ce régime, je ne peux pas prévoir donc si le 19 juin je pourrais continuer ce que j’énonce cette année.
Faites comme vous voudrez, vous encourrez la chance, vous ferez une pétition, je ne sais pas, faites ce qui vous plaît. Voilà donc le point.
C’est évident que comme c’est ce matin même qu’on m’en a averti, je n’ai pas pu mijoter les choses d’une façon telle que je fasse aujourd’hui la conclusion si tant est qu’ à aucune de mes années y’a, à proprement parler une conclusion ce qui est conséquence que ce que je vous énonce ne peut toujours que rester jusqu’à un certain point ouvert, ce n’est pas un privilège. Les choses chaque année restent ouvertes sur un certain nombre de points en suspens. Ce sera d’ailleurs ce sur quoi aujourd’hui j’aurai amplement à m’ étendre.
J’avais rêvé cette nuit que, quand je venais ici, y’avait personne. C’est d’où se confirme le caractère de vœu du rêve. Malgré bien entendu que j’étais… puisque j’avais déjà travaillé au milieu de la nuit, j’étais assez outré puisque je me souvenais aussi dans mon rêve que j’avais travaillé à quatre heures et demie du matin, j’étais assez outré que tout ça doive servir à rien mais c’était quand même la satisfaction d’un vœu, à savoir que dès lors je n’avais plus qu’à me les rouler. Voilà.
Je vais dire, je vais dire la fonction, je vais le dire une fois de plus parce que je me répète, je vais dire une fois de plus ce qui est de mon dire et qui s’énonce : il n’y a pas de métalangage. Quand je dis ça, je parle apparemment du langage de l’être, à part bien entendu que que comme je l’ai fait remarquer la dernière fois, ce que je dis c’est ce qu’il n’y a pas. L’être est autrement dit le non-être n’est pas.
Y’a ou n’y a pas.
Pour moi ce n’est qu’un fait de dit. On suppose l’être à certains mots, individu par exemple, ou substance, c’est même fait pour dire ça qu’on suppose l’être à l’individu entre autres. Ce mot sujet que j’emploie, vous allez le voir, j’y reviendrai, prend évidemment un accent différent du fait de mon discours.
Pour tout dire, je préviens, je me distingue du langage de l’être. Ceci implique qu’il puisse y avoir fiction de mots, je veux dire à partir du mot. Et comme certains peut-être s’en souviennent, c’est de là que je suis parti quand j’ai parlé de l’éthique. Ce n’est pas parce que j’ai écrit des choses qui font fonction de forme du langage que j’assure l’être du métalangage. Car cet être, il faudrait que je le présente comme subsistant par soi, par soi tout seul, langage de l’être.
La formalisation mathématique qui est notre but, notre idéal
pourquoi, parce que seule elle est mathème c’est-à-dire capable de se transmettre intégralement, la formalisation mathématique c’est de l’écrit, et c’est là-dedans que je vais essayer d’avancer aujourd’hui.
Or, elle ne subsiste cette formalisation mathématique, que si j’emploie à la présenter la langue dont j’use. C’est là qu’est l’objection. Nulle formalisation de la langue n’est transmissible sans l’ usage de la langue elle-même. C’est par mon dire que cette formalisation, idéal métalangage, je la fais ex-sister. C’est ainsi que le symbolique ne se confond pas, loin de là, avec l’être, mais qu’il subsiste comme ex-sistence du dire. C’est ce que j’ai souligné dans le texte dit L’Étourdit – d,i,t. –, c’est ce que j’ai souligné de dire que le symbolique ne supporte que l’ex-sistence.
En quoi je l’ai rappelé la dernière fois, c’est une des choses importantes que j’ai dites dans cet exercice, que comme d’habitude j’ai fait plus ou moins pour vous retenir, vous faire entendre, mais il serait peut-être quand même important que vous vous souveniez de l’essentiel. L’essentiel, je l’ai rappelé encore une fois à propos de l’inconscient, l’inconscient se distingue entre tout ce qui a été produit jusqu’alors de discours, qu’il énonce ceci qui est l’os de mon enseignement, que je parle sans le savoir, je parle avec mon corps et ceci sans le savoir. Je dis donc toujours plus que je n’enseigne. C’est là que j’arrive au sens du mot sujet dans cet autre discours. Ce qui parle sans le savoir me fait je, sujet, sujet du verbe certes, mais ça ne suffit pas à me faire être. Ça n’a rien à faire avec ce que je suis forcé de mettre dans l’ être, suffisamment de savoir pour se tenir mais pas une goutte de plus, et c’est ce que jusqu’alors on a appelé la forme.
Dans Platon, la forme c’est ce savoir qui remplit l’être. La forme n’en sait pas plus qu’elle ne dit, elle est réelle, viens-je de dire, en ce sens qu’elle tient l’être dans sa coupe mais à ras bord. Elle est le savoir de l’être, le discours de l’être suppose que l’être sait et c’est ce qui le tient.
Il y a du rapport d’être qui ne peut pas se savoir. C’est lui dont, dans mon enseignement j’interroge la structure, en tant que ce savoir, je viens de le dire impossible, est par-là interdit. C’est ici que je joue de l’équivoque, de l’équivoque qui de ce savoir impossible nous dit qu’il est censuré, défendu, il ne l’est pas si vous écrivez convenablement cet inter-dit, d’un trait d’union entre l’inter et le dit, c’est qu’il est dit entre les mots, entre les lignes et que c’est ça dont il s’agit de…
d’énoncer à quelle sorte de réel nous permet l’accès.
Il s’agit de montrer où va sa mise en forme, ce métalangage qui n’est pas et que je fais ex-sister.
Ce qui ne peut être démontré suggère quelque chose qui peut en être dit de vrai sur le sujet par exemple, entre autre, de l’indémontrable. C’est ainsi que s’ouvre cette sorte de vérité, la seule qui nous soit accessible et qui porte par exemple sur le non-savoir-faire.
Je sais pas comment m’y prendre, pourquoi pas le dire, avec la vérité pas plus qu’avec la femme, puisque j’ai dit que l’une et l’autre, au moins pour l’homme, c’était la même chose, ça fait le même embarras. Il se trouve, c’est accident, que j’ai du goût aussi bien pour l’une que pour l’autre malgré tout ce qu’on en dit.
Cette discordance du savoir et de l’être, c’est ce qui est notre sujet. Ça n’empêche pas qu’on peut dire aussi qu’il n’y en a pas de discordance quant à ce qui mène le je, selon mon titre de cette année, Encore. C’est l’insuffisance du savoir par quoi nous sommes en corps pris, et c’est par là que ce je d’Encore se mène, non pas qu’à en savoir plus il nous mènerait mieux, mais peut-être qu’il y aurait meilleure jouissance, accord de la jouissance et de sa fin. Or, la fin de la jouissance c’est, c’ est ce que nous enseigne tout ce qu’articule Freud de ce qu’il appelle inconsidérément pulsion partielle, la fin de la jouissance est à côté de ce à quoi elle aboutit, c’est à savoir que nous nous reproduisions.
Le je n’est pas un être, c’est un supposé à ce qui parle. Ce qui parle n’a affaire qu’avec ma solitude sur le point du rapport que je ne puis définir qu’à dire comme je l’ai fait qu’il ne peut pas s’écrire. Cette solitude elle, de rupture du savoir, non seulement elle peut s’écrire, mais elle est même ce qui s’écrit par excellence, ce qui d’une rupture de l’être laisse trace. C’est ce que j’ai dit dans un texte, certes non sans imperfections, que j’ai appelé Lituraterre. La nuée du langage me suis-je exprimé métaphoriquement fait écriture. Qui sait si le fait que nous pouvons lire ces ruisseaux que je regardais au retour du Japon, sur la Sibérie, comme traces métaphoriques de l’écriture, n’est pas lié
lier et lire c’est les mêmes lettres faites-y attention
n’est pas lié à quelque chose qui va au-delà de l’effet de pluie dont il n’y a aucune chance que l’animal le lise comme tel.
Bien plutôt est-il lié à cette forme d’idéalisme que je voudrais vous faire entrer dans la tête, non pas certes celui dont parle Berkeley, à vivre dans un temps où le sujet avait pris son indépendance, non pas que tout ce que nous connaissons soit représentation, mais bien plutôt cet idéalisme qui ressortit à l’impossible d’inscrire la relation sexuelle entre deux corps de sexe différent.
C’est par là que se fait l’ouverture par quoi c’est le monde qui vient à nous faire son partenaire. C’est le corps parlant en tant qu’il ne peut réussir à se reproduire que grâce à un malentendu sur sa jouissance et cela c’est dire qu’il ne se reproduit que grâce à un ratage de ce qu’il veut dire, car ce qu’il veut dire comme le dit bien le français, son sens, c’est sa jouissance effective,
c’est à la rater
c’est à dire à baiser
car c’est justement ça qu’il ne veut pas faire, la preuve c’est que quand on le laisse tout seul il sublime tout le temps à tours de bras, il voit la beauté, le bien, sans compter le vrai, c’est encore là comme je viens de vous le dire qu’il est le plus près de ce dont il s’agit, mais ce qui est vrai c’est que le partenaire de l’autre sexe reste l’Autre.
C’est donc à la rater qu’il réussit à être en corps reproduit, sans rien savoir de ce qui reproduit, notamment ceci qui est dans Freud parfaitement sensible, bien sûr ça n’est qu’un bafouillage mais nous ne pouvons pas faire mieux, il ne sait pas si ce qui le reproduit c’est la vie ou la mort. J’ai pas dit ce qu ’il, q.u. apostrophe i,1, j’ai dit ce qui, q.u.i., l.e., il faut séparer.
Oui, il me faut pourtant dire ce qu’il y a de métalangage et en quoi il se confond avec la trace laissée par le langage. C’est par là qu’il fait retour à la révélation du corrélat de la langue, ce savoir en plus de l’être, sa petite chance d’aller à l’Autre, dont j’ai pourtant fait remarquer la dernière fois, c’est l’autre point essentiel, qu’il est ce savoir en plus, passion de l’ignorance, que justement c’est de cela qu’il ne veut rien savoir. De l’être de l’Autre il ne veut rien savoir. C’est bien pour ça que les deux autres passions sont celles qui s’appellent l’amour qui n’a rien à faire contrairement à ce que la philosophie a élucubré avec le savoir, et la haine qui est bien ce qui a le plus de rapport avec l’être ce qui s’en approche le plus, que j’appelle l’ex-sister. Rien ne concentre plus de haine que ce dire où se situe ce que j’appelle l’ex-sistence.
L’écriture est une trace où se lit un effet de langage.
Quand vous gribouillez quelque chose et moi aussi je m’en prive certes pas, c’est avec ça que je prépare ce que j’ai à dire, et c’est remarquable qu’il faille de l’ écriture s’assurer. C’est pas le métalangage, quoiqu’on puisse lui faire remplir une fonction qui y ressemble mais qui n’en reste pas moins, au regard de l’Autre où le langage s’inscrit comme vérité, qui n ’en reste pas moins tout à fait seconde. Car rien de ce que je pourrais au tableau vous écrire des formules générales qui lient au point où nous en sommes l’énergie à la matière, par exemple la dernière formule d’Heisenberg, rien ne tiendra tout ça si je ne le soutiens pas d’un dire qui est celui de la langue et d’une pratique qui est celle de gens qui donnent des ordres au nom d’un certain savoir.
Alors quand vous gribouillez, ma foi comme on le dit c’est toujours sur une page et c’est avec des lignes, et nous voilà plongés tout de suite dans l’histoire des dimensions. Comme ce qui coupe une ligne c’est le point et que le point a zéro dimension, la ligne sera définie d’en avoir deux… Comme ce qui coupe… la ligne sera définie d’en avoir une…
comme ce que coupe la ligne, c’est une surface, la surface sera définie d’ en avoir deux. Comme ce que coupe la surface c’est l’espace, l’espace en aura trois.
Seulement, c’est là que prend sa valeur le petit signe que j ’ai écrit là-haut. Je veux dire celui qu’il faut que je distingue de celui que j’ai écrit au-dessous. Ils sont séparés. Vous pouvez remarquer que c’est quelque chose qui a tous les caractères d’écriture ça pourrait aussi bien être une lettre. Seulement comme vous écrivez cursivement, il vous vient pas à l’idée d’arrêter la ligne avant qu’elle en rencontre une autre pour la faire passer dessous, la supposer passer dessous, parce qu’il s’agit dans l’écriture de tout autre chose que de l’espace à trois dimensions 148.
Cette ligne coupée ici, ai-je dit, veut dire qu’elle passe sous l’autre. Ici c’est au-dessus parce que c’est l’autre qui s’interrompt, c’est ce qui produit, encore qu’il n’y ait pas ici qu’une ligne, cette chose qui se distingue de ce que serait un simple rond, un rond de ficelle si ça existait. Ça s’en distingue en ce sens que quoiqu’il n’y ait qu’une seule ficelle, ça fait un nœud.
C’est quand même tout autre chose cette ligne que la définition que nous en avons donnée tout à l’heure au regard de l’espace, c’est-à-dire en somme une coupure, ce qui fait un trou, un intérieur, un extérieur de la ligne.
Cette autre ligne, cette ficelle, comme je l’ai appelée ça ne s’incarne pas si facilement dans l’espace. La preuve, c’est que la ficelle idéale, la plus simple, ça serait un tore. Et on a mis très longtemps à s’apercevoir grâce à la topologie que ce qui s’enferme dans un tore, c’est quelque chose qui n’a absolument rien à voir avec ce qui s’enferme dans un cube. Il ne s’agit pas de couper le tore, car quoique vous fassiez avec la surface d’un tore vous ne ferez pas un nœud. Mais par contre avec le lieu du tore, comme ceci vous le démontre, vous pouvez faire un nœud. C’est en quoi, permettez-moi de vous le dire, le tore c’est la raison c’est ce qui permet le nœud. C’est bien en quoi ce que je vous montre, ce tore tortillé c’est l’image aussi simple et aussi sec que je peux vous la donner de ce que j’ai évoqué l’autre jour comme la trinité, une et trois d’un seul jet.
Il n’en reste pas moins que c’est à en refaire trois tores par le petit truc que je vous ai déjà montré sous le nom de nœud borroméen que nous allons pouvoir opérer, dire quelque chose sur ce qu’il en est de l’usage du premier nœud. Naturellement il y en a qui étaient pas là quand j’ai parlé l’année dernière, du côté de février, du nœud borroméen.
Nous allons tâcher aujourd’hui de vous faire sentir l’importance de cette histoire et en quoi elle a affaire à l’écriture pour autant que je l’ai définie comme ce que laisse de traces le langage.
Le nœud borroméen consiste en ceci que nous y avons affaire avec ce qui ne se voit nulle part, à savoir un vrai rond de ficelle. Parce que figurez-vous que quand on trace une ficelle on n’arrive jamais à ce que sa trame joigne ses deux bouts. Pour que vous ayez un rond de ficelle, il faut que vous fassiez un nœud, nœud marin de préférence (dans la salle on rit). Je vois pas ce que ça a de bouffon, bon ! Ah ! faisons le nœud marin, si vous croyez que c’est facile essayez-vous-y vous-même, ça fait toujours un certain embarras. Bon ! Enfin, malgré tout, j’ai essayé ces jours-ci d’en prendre l’habitude et il y a rien de plus facile que de le rater. Voilà ! Grâce au nœud (applaudissements), vous avez là un rond de ficelle.
Le problème qui est posé par le nœud borroméen est celui-ci : comment faire, quand vous avez fait vos ronds de ficelle, pour que, pour que quelque chose dans le genre de ce que vous voyez dans le haut, à savoir un nœud, pour que ces trois ronds de ficelle tiennent ensemble, et de façon telle, de façon telle que si vous en coupez un ils soient tous libres, je veux dire les trois les trois ce qui n’est rien. Car le problème c’est de faire qu’avec un nombre quelconque, quelconque de ronds de ficelle, quand vous en coupez un, tous les autres sans exception, soient désormais libres, indépendants.
Voici par exemple le cas, j’ai déjà l’année dernière mis ça au tableau.
Naturellement, comme j’ai fait une petite faute, ce n’est pas tout à fait satisfaisant mais ça va le devenir. Rien n’est plus facile dans cet ordre que de faire une faute. Ah ! Encore ma faute !
Tel que vous le voyez là, tel que vous le voyez là inscrit, il vous est facile de voir que comme ces deux ronds de ficelle sont construits de telle sorte qu’ils sont pas noués l’un à l’autre, c’est uniquement par le troisième qu’ils se tiennent, ce que curieusement je ne suis pas arrivé à reproduire avec mes ronds de ficelle. Mais Dieu merci, j ’ai quand même un autre moyen de le faire que de reproduire ce que je fais au tableau, à savoir de le manquer. (à son assistante : ouvrez moi vous serez gentille. Celui-là) Je vais tout de suite vous donner le moyen de façon complètement rationnelle et compréhensible…, voilà, voilà donc un rond de ficelle, en voilà un autre.

Vous passez le second rond dans le premier et vous le pliez comme ça. Il suffira dès lors que d’un troisième rond vous preniez le second, pour que ces trois soient noués, et noués de telle sorte qu’il suffit bien évidemment que vous sectionniez un des trois pour que les deux autres soient libres.
Supposez chers amis que je vous enlève celui-ci, celui-ci que je viens de reprendre, hein, vous voulez le dernier, c’est celui-là que vous voulez, mais c’est tout à fait la même chose, c’est tout à fait la même chose pour la simple raison que celui-là, que je vous ai représenté comme plié et qui a en somme deux oreilles dans lesquelles passe le troisième, il est absolument symétrique de l’autre côté, à savoir que par rapport au troisième il a aussi deux oreilles que prend le premier.
Non seulement ceci, ne croyez pas vous savez que ce soit inutile n’est-ce pas, tous ces petits cafouillages, ce n’est pas si familier que la façon dont je suis amené à l’expliquer, avec des ratages justement, ne soit pas ce qui peut vous le faire entrer dans la tête. Car il faut que je vous le montre, parce qu’après tout, il n’y a que comme ça que ça peut entrer. Après le premier pliage, vous pouvez avec le troisième, à condition ici de faire un nœud, faire un pliage nouveau. Et à celui-ci un quatrième, un quatrième qui est comme le premier étant ajouté, vous voyez qu’il reste tout aussi vrai avec quatre qu’avec trois qu’il suffise de couper un de ces nœuds pour que tous les autres soient libres entre eux. Vous pouvez en mettre un nombre absolument infini, ce sera toujours vrai.
Néanmoins, cette histoire qui rend simple le nœud borroméen en ce sens qu’ ici par exemple vous pouvez parfaitement toucher en quoi ce sont les deux parties de cet élément qui font oreille, celle-ci et celle-ci, et qu’en somme en le tirant avec l’autre, c’est ce rond qui se plie en deux, ici et ici passent, sont les deux oreilles, et ce cercle là, qui ira lui, laissons celui que nous pourrons dans cette occasion, mais uniquement dans cette occasion appeler premier, qui restera à l’état de rond, de rond-soutien du premier rond plié.
A cette intuition sensible, en quelque sorte, de la fonction des ronds, vous pouvez constater qu’il suffit d’en couper un quelconque, que ce soit un du milieu ou un des deux extrémités, pour que tout ce qu’il y a de nœuds pliés, du même coup, soit d’entre-soi libéré. La solution est donc absolument générale.
Cela ne veut pas dire que pour un nombre quelconque de ronds de ficelle, on pourra faire une disposition aussi relativement élégante par sa relative symétrie que celle que j’ai fait au tableau, à savoir que ces trois ronds soient strictement, les uns par rapport aux autres, d’une forme‚ équivalente. Ça sera certainement plus compliqué et ceci dès qu’on sera arrivé à quatre, cela nous montrera bien souvent des effets de torsion qui ne nous permettront pas de les maintenir à l’état de ronds.
Néanmoins, ce que je veux à cette occasion vous faire sentir c’est que partant des ronds nous avons affaire à quelque chose qui ne se distingue que d’être l’Un. C’est très précisément d’ailleurs, en quoi un vrai rond de ficelle sans nœud c’est très difficile à faire. Mais c’est certainement la plus éminente représentation de quelque chose qui ne se soutient que de l’Un très précisément en ce sens que ça n’enferme rien qu’un trou. Et que pourquoi ai-je fait intervenir dans l’ancien temps le nœud borroméen, c’est très précisément pour traduire la formule : Je te demande quoi ? de refuser ce que quoi ? Ce que je t’offre, c’est à dire quelque chose qui au regard de ce dont il s’agit, et vous savez ce que c’est, c’est à savoir l’objet petit a. L’objet petit a n’est aucun être, l’objet petit a c’est ce que suppose, suppose de vide une demande, dont en fin de compte, ce n’est qu’à la définir comme située par la métonymie, c’est à dire par la pure continuité assurée du commencement ou début de la phrase, que nous pouvons imaginer ce qu’il peut en être d’un désir qu’aucun être ne supporte, je veux dire qui est sans autre substance que celle qui s’assure des nœuds mêmes. Et la preuve, c’est que, énonçant cette phrase : je te demande de refuser ce que je t’offre, je n’ai pu que la motiver de ce, ce n’est pas ça, dont j’ai parlé, que j’ai repris la dernière fois, et qui veut dire que dans le désir de toute demande il n’y a que la requête de ce quelque chose qui au regard de la jouissance qui serait satisfaisante, qui serait la Lustbefriedigung supposée dans ce qu’on appelle également improprement dans le discours psychanalytique 1a pulsion génitale, celle où s’inscrirait un rapport qui serait le rapport plein, le rapport inscriptible entre ce qu’il en est de l’Un avec ce qui reste irréductiblement l’Autre.
C’est en quoi j’ai insisté sur ceci, c’est que le partenaire de ce je qui est le sujet, le sujet de toute phrase de demande, c’est que son partenaire est non pas l’Autre mais ce quelque chose qui vient se substituer à lui sous la forme, sous la forme de cette cause du désir que j’ai cru pouvoir diversifier, diversifier et ce n’est pas sans raison, en quatre, en tant qu’il se constitue selon la découverte freudienne, en tant qu’il se constitue diversement de l’objet de la succion, de l’objet de l’excrétion, du regard et aussi bien de la voix. C’est en tant que substitut de ce qu’il en est de l’Autre que ces objets sont réclamés, sont faits cause du désir.
Comme je l’ai dit tout à l’heure, il semble que le sujet se représente les objets inanimés très précisément en fonction de ceci qu’il n’y a pas de relation sexuelle. Il n’y a que les corps parlant ai-je dit, qui se font une idée du monde comme tel. Et à cet endroit on peut le dire, que le conte 149, le monde comme tel, le monde de l’être plein de savoir, ce n’est qu’un rêve, un rêve du corps en tant qu’il parle. Il n’y a pas de sujet connaissant, il y a des sujets qui se donnent des corrélats dans l’objet petit a, corrélats de paroles jouissantes en tant que jouissance de parole. Que coincent-elles d’autre que d’autres uns ? Car, comme je vous l’ai fait remarquer tout à l’heure, il est clair que cette bilobulation, cette transformation du rond de ficelle en oreilles, il peut se faire de façon strictement symétrique, ce qui est même ce qui arrive dès qu’on arrive au niveau de quatre, c’est-à-dire que les deux ronds que représentent mes doigts à l’extrémité de ceux-ci seraient en fonction, il y en aurait quatre.
La réciprocité, pour tout dire entre le sujet et l’objet petit a est totale. Pour tout être parlant la cause de son désir est strictement quant à la structure‚ équivalente si je puis dire, à sa pliure, à ce que j’ai appelé sa division de sujet. Et c’est bien ce qui nous explique que si longtemps le sujet a pu croire que le monde en savait autant que lui, c’est qu’il est symétrique, c ’est que le monde, ce que j’ai appelé la dernière fois le penser, c’est l’équivalent, c’est l’image en miroir de la pensée. C’est bien en quoi le sujet, pour autant qu’il fantasme, il n’y a, jusqu’à l’avènement de la science la plus moderne, il n’y a rien eu que fantasme quant à la connaissance, et c’est bien ce qui a permis cette échelle d’êtres grâce à quoi était supposé dans un être dit Être Suprême ce qui était le bien de tous, ce qui est aussi bien l’équivalent, l’équivalent de ceci que l’objet petit a peut être dit, comme son nom l’indique, écrivez-le petit a entre parenthèses, mettez sexué après, et vous savez que l’Autre ne se présente pour le sujet que sous une forme (a)sexuée. C’est-à-dire que tout ce qui a été le support, le support substitut, substitut de l’Autre sous la forme de l’objet de désir, tout ce qui s’ est fait de cet ordre, est (a)sexué. Et c’est très précisément en quoi l’ Autre comme tel reste, reste non sans que nous puissions y avancer un peu plus, reste dans la doctrine, la théorie freudienne, un problème,
celui qui s’est exprimé en ceci que répétait Freud : que veut la femme ?
la femme étant dans l’occasion l’équivalent de la vérité. C’est en quoi cette équivalence que j’ai produite est justifiée.
Est-ce que nous ne pouvons pas pourtant par cette voie
cette voie de ce que j’ai distingué comme l’Un à prendre comme tel, en ce sens qu’il n’y a rien d’autre dans cette figure du rond de ficelle, qui a pourtant son intérêt de nous offrir, de nous offrir le quelque chose que rejoint sans doute l’écriture,
l’exigence en effet que j’ai produite sous le nom de nœud borroméen, à savoir de trouver une forme,
cette forme supportée par ce support mythique qu’est le rond de ficelle, mythique ai-je dit car on ne fait pas de rond de ficelle fermé, ceci est un point tout à fait important.
Quelle est cette exigence que j’ai énoncée sous le nom
de nœud borroméen ?
C’est très précisément ceci qui distingue, qui distingue ce que nous trouvons dans le langage, dans la langue courante, et qui se supporte de la métaphore très répandue de la chaîne, contrairement aux ronds de ficelles.
Des éléments de chaîne, ça se fait ça se forge, ce n’est pas très difficile d’imaginer comment ça se fait, on tord du métal jusqu’au moment où on peut arriver à la souder, et la chaîne est ainsi quelque chose qui peut avoir sa fonction pour représenter l’usage de la langue. Sans doute n’est-ce pas un support simple, il faudrait dans cette chaîne faire des chaînons qui iraient s’accrocher à un autre chaînon un peu plus loin avec deux ou trois chaînons flottants intermédiaires, et comprendre aussi pourquoi une phrase a une durée limitée.
Or tout ceci la métaphore ne peut pas nous le donner.
Il est néanmoins frappant qu’à prendre les supports de ronds de ficelle que je vous ai dit il y en avait quand même dans ce que je vous ai rendu sensible, un premier et un dernier. Ce premier et ce dernier étaient des ronds simples qui franchissaient, qui perçaient si je puis dire les deux, ce que j’appelle, vous voyez la difficulté de parler de ces choses, ce que j’appelle les lobes d’oreilles des ronds repliés. C’était donc deux nœuds simples qui à la fin se trouvaient faire quelque chose comme le début et la fin de la chaîne.
Il reste ceci. Il reste ceci, c’est que ces deux ronds initiaux terminaux, rien ne nous empêcherait de les confondre. C’est à savoir que les ayant coupé, coupé ce qui est imaginaire, il suffit de les défaire, d’ en faire passer un seul à prendre les quatre lobes
ainsi résumés dans un cas où il y en a que deux, mais la situation serait exactement la même s’il y en avait un nombre infini. Chose à remarquer nous n’aurions, pour m’exprimer vite, nous n’aurions dans ce cas…
quand même encore une différence. Ce n’est pas parce que nous aurions conjoint les deux derniers nœuds que toutes les articulations seraient les mêmes
car ici ils sont affrontés deux par deux, il y a donc quatre brins à faire nœud
alors qu’ici à prendre, à prendre mon cercle unique, vous auriez le support de ce cercle et quatre brins à passer, ce qui ferait un affrontement non pas de deux à deux qui font quatre mais de quatre à un qui font cinq. Et donc on pourrait dire que même ce qui serait alors, puisque ici vous n’avez que deux éléments, le troisième élément, le troisième élément dans son rapport topologique n’aurait pas le même rapport avec les deux autres que les deux autres entre eux. Et comme tels, à simple inspection des nœuds en fonction, le troisième élément se distinguerait des autres.
Je pense en avoir assez dit sur la symétrie des rapports du premier et du deuxième, puisque le dernier je l’ai appelé le troisième. Cette symétrie tient encore, cette symétrie tient encore si vous unifiez le troisième rond avec un quelconque des deux autres. Simplement vous aurez alors une figure comme celle-ci, celle qui affronte un simple rond avec ce que j’ appelle le huit intérieur.
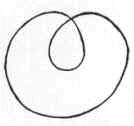
Vous aurez donc eu l’épanouissement de l’Autre mais au prix de la surgescence de quelque chose qui est le huit intérieur et qui comme vous le savez est ce dans quoi je supporte la bande de Moebius, autrement dit ce dont en quoi dans un strict support de cette voie que j’essaie pour vous de frayer de la fonction du nœud, s’exprime par le huit intérieur. Je ne peux ici que l’amorcer, pourquoi, parce que j’ai encore à avancer quelque chose qui me paraît, avant que je vous quitte, capital. Si je vous ai donné la solution des nœuds borroméens par cette enfilade de chaînes pliées sous la forme de ces ronds qui redeviennent totalement indépendants pour peu que vous en coupiez un seul, à quoi ceci peut-il servir ?
Contrairement à ce que vous voyez dans le langage, c’est à savoir ce qui vous est très simplement matérialisé et ce n’est pas non plus très difficile, très difficile d’en trouver un exemple et pas pour rien dans la psychose. Souvenez-vous de ce qui hallucinatoirement peuple la solitude de
Schreber :
Nun will ich mich…, ce que je traduis : maintenant je vais me …, c’est un futur. Ou encore
sie sollen nämlich…. vous devez quant à vous …
Ces phrases interrompues que j’ai appelées (long silence) message de code, ces phrases interrompues laissent en suspens je ne sais quelle substance. Á quoi peut nous servir cette exigence d’une phrase quelle qu’elle soit, qui soit telle qu’ayant sectionné l’un, c’est-à-dire retiré d’l’Un de chacun de ces chaînons, tous les autres du même coup soient libres ?
Est-ce que ce n’est pas là le meilleur support que nous puissions donner de ce par quoi procède ce langage que j’ai appelé mathématique ?
Le propre du langage mathématique une fois qu’il est suffisamment resserré quant à ses exigences de pure démonstration, et très précisément ceci de tout ce qui s’en avance, s’en avance non pas tant dans le commentaire parlé mais dans le maniement des lettres, suppose ceci qu’il suffit qu’une ne tienne pas pour que tout le reste, tout le reste des autres lettres, non seulement ne constituent par leur agencement rien de valable, mais se dispersent. Et c’est très précisément en ceci que le nœud borroméen peut nous servir de meilleure métaphore quant à ce qu’il en est d’une exigence qui est celle-ci : c’est que nous ne procédons que de l’Un.
L’Un engendre la science, non pas au sens où quoique ce soit s’en mesure, ce n’est pas ce qui se mesure dans la science contrairement à ce qu’on croit, qui est l’important. Ce qui fait le nerf original, ce qui distingue la science, la science moderne de la science de la réciprocité entre le nous / no et le monde, entre ce qui pense et ce qui est pensé, c’est justement cette fonction de l’Un, en tant que l’Un n’est pas là, n’est là pouvons-nous supposer, que pour représenter ce qu’il en est justement de ce que l’Un est seul, de ce que l’Un ne se noue véritablement avec rien de ce qui ressemble à l’Autre sexuel, que c’est au contraire de la chaîne entre des uns qui sont tous faits de la même façon, de n’être rien d’autre que de l’Un.
Quand j’ai dit y’a d’l’Un et que j’y ai insisté, que j’ai vraiment piétiné ça comme un éléphant pendant toute l’année dernière, vous voyez ce que je fraye et ce à quoi je vous introduis.
Comment alors quelque part mettre comme telle la fonction de l’Autre, comment si jusqu’à un certain point c’est simplement des nœuds de l’Un que se supporte ce qui reste quand ça s’écrit de tout langage, comment poser une différence car il est clair que l’Autre ne s’additionne pas à l’Un, l’Autre seulement s’en différencie. S’il y a quelque chose par quoi il participe à l’Un c’est que bien loin qu’il s’additionne, ce dont il s’agit concernant l’Autre c’est comme je l’ai dit déjà mais il n’est pas sûr que vous l’ayez entendu c’est que l’Autre c’est l’Un en moins. C’est pour ça que dans, dans tout rapport de l’homme avec une femme, celle qui est en cause c’est sous l’angle de l’Une en moins qu’elle doit être prise.
Je vous avais déjà indiqué ça un petit peu à propos de Don Juan, mais bien entendu il n’y a qu’une seule personne je crois, ma fille nommément, qui s’en soit aperçu. Néanmoins pour simplement aujourd’hui amorcer ce que je pourrais vous dire d’autre, je vais vous montrer quelque chose. Car il ne suffit pas d’avoir trouvé une solution générale à ce qu’il en est du problème pour un nombre infini des nœuds borroméens, il faudrait que nous ayons le moyen de montrer que c’est la seule solution. Or nous en sommes à ceci jusqu’à ce jour qu’ il n’y a aucune théorie des nœuds. Qu’est-ce que ça veut dire, ça veut dire ceci que très précisément, au nœud ne s’applique jusqu’à ce jour aucune formalisation mathématique qui permette, en dehors de quelques petites fabrications de petits exemples tels que ceux que je vous ai montrés, de prévoir qu’une solution, celle que je viens de donner n’est pas simplement une solution ex-sistante, mais qu’elle est nécessaire, qu’elle ne cesse pas comme je le dis pour définir le nécessaire, qu’elle ne cesse pas de s’écrire. Or, il suffit que tout de suite je vous montre quelque chose que bien sûr je vais écrire au tableau, parce que vous savez pas le tintouin que ça me donne de mettre tout ça sur le papier d’une façon que je tiens à votre disposition, qui sera aussi bien photographié dans un prochain article mais qui en demande un certain.
Il suffit que je vous fasse ça :
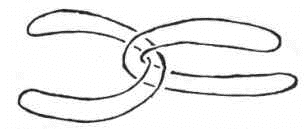
C’est embêtant que les autres, les autres nœuds soient là.
Regardez ça.
Je viens de faire passer deux de ces ronds l’un dans l’autre d’une façon telle qu’ils font ici non pas du tout ce re-pliage que je vous ai montré tout à l’heure mais simplement un nœud marin. Comme ils sont de ce fait même, puisque je viens de les agencer fermés, comme ils sont de ce fait même parfaitement séparables l’ un de l’autre, vous devez penser que, si simplement ce qui m’est tout aussi possible je fais avec un cercle qui suit le même nœud marin, il suffit que j’approche de ceux-là un autre, ici je peux faire la même chose avec un troisième rond. J’aurai encore un nœud marin, peu importe qu’il soit face à face avec le premier ou qu’il soit strictement dans la file, c’est-à-dire que ce qui passe devant, passe devant également le suivant.
Je peux en faire un nombre infini et même fermer le cercle que cela fera, le fermer simplement. Pour le dernier, pour le dernier bien sûr, il ne sera pas séparable, il faudra que ce dernier je le passe entre les deux du bout de ce que j’aurai déjà construit, et que je le passe en faisant un nœud. Non pas en l’introduisant comme je viens de faire pour ces deux-là. Il n’en restera pas moins que voilà une autre solution tout aussi valable que la première, car que je sectionne un quelconque de ceux que j’aurai agencés ainsi, tous les autres du même coup seront libres, et pourtant ce ne sera pas la même sorte de nœud.
Je vous ai passé à l’occasion ceci que tout à l’heure, pour le n œud que je vous ai montré ainsi, en vous disant qu’aussi bien il y avait quelque nécessité que celui dans lequel j’ai conjoint le premier et le dernier rond, quelque nécessité d’une différence, il n’en est, en réalité, rien. Car je vous le fais remarquer, au moment où je viens de vous montrer les autres, à savoir ce que j’ai appelé la prise en forme de nœud marin, vous voyez très bien à ceci que même le dernier, ce dernier dont je vous ai dit que l’affrontement était de un à quatre, et que du même coup il y avait cinq brins dans le coup, que même le dernier je peux le faire exactement semblable à tous ceux-là, qu’il n’y a à ça aucune difficulté, et qu’ainsi j’aurai aussi de cette façon résolu sans introduire aucun point privilégié la question du nœud borroméen, pour un nombre x et aussi bien infini de ronds de ficelle.
Est-ce que ce n’est pas dans cette possibilité de différence, puisque aussi bien il n’y a aucune analogie topologique entre l’une et l’autre de ces façons de nouer les ronds de ficelle ? Est-ce que c’est dans cette topologie différente, une que nous pouvons exprimer ici à propos des nœuds marins, c’est une topologie de torsions, disons, par rapport aux autres, qui seraient simplement de flexions.
Est-ce que nous pouvons user de ceci pour,
car il ne serait pas contradictoire de prendre même ceci dans un nœud marin ?
C’est très facile à faire, faites-en l’épreuve.
Très exactement voici la façon dont la chose fléchit, se prend au nœud marin.
Où mettre la limite de cet usage des nœuds pour arriver à la solution de ce qu’est ceci :
la section d’un quelconque de ces ronds de ficelle entraîne la libération de tous les autres, c’est à dire nous donne le modèle de ce qu’il en est à partir de cette formalisation mathématique, celle qui substitue à la fonction d’un nombre quelconque ce qu’on appelle une lettre. Car la formalisation mathématique ce n’est pas autre chose. Que vous écriviez que quelque chose, que vous écriviez que quelque chose, l’énergie 150, ce soit un demi de mv2.
qu’est que ça veut dire, ça veut dire que quelque soit le nombre d’uns que vous mettiez sous chacune de ces lettres, vous êtes soumis à un certain nombre de lois qui sont des lois de groupe telles que l’addition, la multiplication…
Voilà la question que j’ouvre et qui est faite pour vous annoncer s’il faut, ce que j’espère, ce que je peux éventuellement vous transmettre concernant ce qui s’écrit.
Ce qui s’écrit, en somme, qu’est-ce que ça serait, les conditions de la jouissance.
Et ce qui se compte, qu’est-ce que ça serait, les résidus de la jouissance ! Car aussi bien cet a, a-sexué, est-ce que ce n’est pas de le conjoindre avec ce qu’elle a de plus de jouir étant Autre de ne pouvoir être dite qu’Autre que la femme l’offre sous l’espèce de l’objet petit a ?
L’homme croit créer
croyez bien que je vous dis pas ça au hasard
croit – croit – croit, bon !
il crée – crée – crée
et il crée – crée – crée la femme. Ouais !
En réalité il la met au travail, mais au travail de l’Un et c’est bien en quoi cet Autre pour autant que s’y inscrit l’articulation du langage, c’est-à-dire la vérité, l’Autre pourra être barré, barré de ceci que j’ai qualifié tout à l’heure de l’Un en moins. Le S de A en tant qu’il est barré :
S A
c’est bien cela que ça veut dire, et c’est en quoi nous en arrivons à poser la question de faire de l’Un quelque chose qui se tienne, c’est-à-dire qui se compte sans être.
La mathématisation seule atteint un réel et c’est en quoi c’est compatible avec notre discours, discours analytique, un réel qui précisément s’évade qui n’a rien à faire avec ce que la connaissance traditionnelle a supporté, c’est-à-dire non pas ce qu’elle croit, la réalité mais bien de fantasme.
Le réel c’est le mystère du corps parlant, c’est le mystère de l’inconscient.
Notes
148 Les notes dont nous disposions ne reproduisaient pas les dessins des nœuds. Nous avons donc utilisé les dessins de la version Seuil, sauf pour le nœud de la p. 10 qui est faux dans la version Seuil. Nous avons utilisé le bon nœud rétabli par Soury et Thomé dans Chaînes et nœuds deuxième partie, texte 58, p. 4.
149 Lacan dit « conte ». Lapsus ?
150 Lapsus ?
Index
NOMS PROPRES
- Berkeley - p. 4
- Don Juan - p. 16
- Freud - p. 5
- Heisenberg - p. 5
- Japon - p. 4
- Platon - p. 3
- Schreber - p. 15
- Sibérie - p. 4
OUVRAGES CITÉS
- L’Étourdit - p. 3
- Lituraterre - p. 4
- Encore - p. 4